The terms of trade can be thought of as a weighted average of the price of export categories relative to the aggregate import price level, with the weights (hereafter volume shares) equal to the respective volume of the export categories as a share of the total export volume:
![]() (1)
(1)
where at time t: PXt is the implicit price deflator for aggregate goods and services exports; PMt is the implicit price deflator for aggregate imported goods and services; n is the number of export categories, Xit is the volume of export category i; Xt is the volume of aggregate goods and services exports; and PXit is the implicit price deflator for export category i.
Forecasts of the terms of trade therefore require estimates of the volume shares of all export categories and the price of each export category relative to the aggregate import price level (hereafter relative export price). With the exception of rural and non-bulk non-rural commodities, we forecast relative export prices directly. For rural and non-bulk commodities we forecast export price levels, which require a forecast of the aggregate import price level to generate relative export prices. This section outlines the projection methodology for aggregate import prices. Since import prices are modelled in aggregate, import volumes are not required for the analysis of the terms of trade.
Analytical framework
The theoretical framework underpinning the modelling of import prices is motivated by previous Australian research undertaken by Dwyer and Lam (1994), and updated work by Chung, Kohler and Lewis (2011) and Beames and Kouparitsas (2013), which suggests Australian households and producers are price takers facing an import price equal to the exchange rate adjusted foreign cost of a good or service (i.e. there is complete first-stage pass-through of foreign cost and exchange rates to import prices). Given that Australia is a significant importer of oil, and oil prices display different behavior to the other goods import prices, aggregate import prices are modelled as a weighted average of oil prices and a trade-weighted aggregate of foreign consumption prices, with the relative weights determined by the model.
A deterministic time trend is also included in the model to account for the observed trend decline in the price of Australian goods relative to exchange rate adjusted foreign goods prices over the early part of the data sample. This trend decline reflects the composition of Australian imported goods which is weighted towards capital intensive goods. The price of capital goods has tended to grow at a slower rate than the broader consumption basket used to model foreign prices for various reasons, including the realisation of global economies of scale in the production of manufactured goods. More recent data suggest this trend decline has weakened significantly and is likely to be reversed in the medium-run as emerging market economies shift away from export-oriented production. In keeping with Treasury’s broader projection methodology, which assumes domestic and foreign expenditure prices (converted to $A) grow at a constant annual rate of inflation of 2.5 per cent, all deterministic trends are held constant over the projection period.
The resulting imports price equation is as follows:
![]() (2)
(2)
where at time t: PCONFt is the trade-weighted foreign consumption price index; ETWIt is the trade-weighted exchange rate index; POILFt is the foreign currency denominated price of oil; β1 is the share of non-oil goods in the import basket; and TRENDt is a linear time trend.
Data
Historical annual (financial year basis) aggregate import price data are sourced from the Australian Bureau of Statistics (ABS) national accounts.
Detailed individual foreign country consumption prices are sourced from various national statistical agencies and other commercial data providers for the period to 2012-13. Forecasts of individual foreign country consumption prices from 2012-13 to 2014-15 are based on detailed bottom-up analysis. These forecasts are then weighted according to the respective countries’ share of aggregate imports to form a trade-weighted foreign consumption price index forecast. This index is assumed to grow at 2.5 per cent, consistent with Treasury’s projection period annual inflation rate assumption.
The historical trade-weighted nominal exchange rate index is sourced from the Reserve Bank of Australia (RBA), while the forecast assumes a constant nominal exchange rate. This implies complete pass-through of nominal exchange rate movements to all export and import prices. The sensitivity of the forecasts to this assumption is explored in Appendix A.
Oil import price forecasts are consistent with the oil export price forecasts derived below (Section 7). Consistent with other non-rural non-bulk commodities exports, the oil export price forecast from 2014-15 to 2022-23 is the mean price prediction of Consensus Economics (2013). From 2022-23 real oil prices are held constant (i.e., oil prices grow at an annual inflation rate of 2.5 per cent).
Parameter estimation and calibration
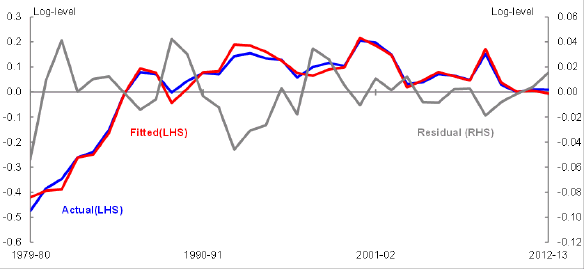
The long-run price equations are estimated using standard econometric techniques. The resulting estimates reported in Table 1 suggest that roughly 90 per cent of the import basket is non-oil goods (β1). It was necessary to introduce an additional trend post 1999-00 to take account of an otherwise unexplained deceleration in the trend decline of Australian imports goods prices relative to exchange rate adjusted foreign goods prices (β3) and a similarly otherwise unexplained level shift over the same time period (α1). According to these estimates the trend decline in import prices relative to foreign consumption prices was 2.4 per cent up to 1999-00 and 1.4 per cent thereafter. Chart 2 shows that the full sample and post 1999-00 trends render the model’s residuals stationary.
Table 1: Import price equation parameters
Method: Least Squares
Sample: 1979-80 2012-13
| Coefficient | Std. Error | t-Statistic | Prob. | |
|---|---|---|---|---|
| α0 | 4.812444 | 0.227857 | 21.12047 | 0.0000 |
| β1 | 0.894277 | 0.021328 | 41.93038 | 0.0000 |
| β2 | -0.023627 | 0.001855 | -12.73638 | 0.0000 |
| β3 | 0.009407 | 0.003977 | 2.365152 | 0.0249 |
| α1 | -0.054515 | 0.022308 | -2.443766 | 0.0209 |
| R-squared | 0.983422 | Mean dependent var | 0.012617 | |
| Adjusted R-squared | 0.981135 | S.D. dependent var | 0.167044 | |
| S.E. of regression | 0.022943 | Akaike info criterion | -4.576523 | |
| Sum squared resid | 0.015266 | Schwarz criterion | -4.352058 | |
| Log likelihood | 82.80089 | Hannan-Quinn criter. | -4.499974 | |
| F-statistic | 430.0723 | Durbin-Watson stat | 1.252388 | |
| Prob (F-statistic) | 0.000000 | |||
Source: Authors’ calculations.
Chart 2: Import price equation fitted values and residuals
Source: Authors’ calculations.