Econometric method
Empirical labour demand model
Following other researchers we estimate Australian labour demand using an error-correction approach. The long-run desired level of employment is determined by the relationship derived above (8), with the resulting error correcting term captured by the expression in [ ] brackets in equation (9) below. The speed at which actual employment approaches its desired level is determined by δ < 0. Short-run dynamics are captured by the addition of lagged first differences of log employment, and contemporaneous and lagged first differences of log output and log real wages. The general error-correcting model we consider is as follows:
 (9)
(9)
Identifying and estimating labour-augmenting technical change
Before we can take this model to the data we must impose additional assumptions to identify labour-augmenting technical change Xt, which is an unobserved component. Neoclassical growth theory offers a guide to the general nature of this process. According to this theory, labour-augmenting technical change has the same trend as the observed real wage and labour productivity (that is, output per worker). If this prediction holds in the data, Xt can simply be estimated as a common trend of labour productivity and the real wage. In contrast to the theory, Chart 1 shows that over the estimation period (1972-2011), productivity has grown at a faster rate than the real wage. This suggests the common trend approach would not be fruitful as there appears to be an additional stochastic trend driving the real wage.
Chart 1: Real wages and average labour productivity
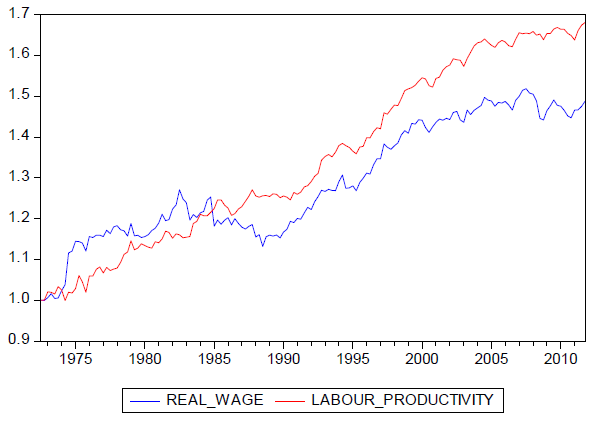
Work-in-progress by Treasury on wage determination suggests that the gap between productivity and real wage growth was due to the rapid rise in unemployment over the 1980s which weakened the bargaining power of employed workers.7
Australian labour demand research (see, for example, Lewis and MacDonald (2002)) has typically overlooked this issue by assuming that Xt can be identified as the trend that causes the term in [ ] to be a cointegrating relationship (that is, the common trend of labour productivity and real wages). Specifically, they have assumed that Xt is a deterministic linear time trend:
![]() (10)
(10)
where: μ is a constant; and λ is the trend growth rate. Substituting (10) into (9) implies the following error correction model:
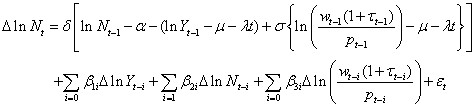 (11)
(11)
While this is a valid econometric approach it can only yield an estimate of the growth rate of labour augmenting technical change if labour productivity and real wages have the same trend. To see this it is important to note that in the context of the model λ is estimated as a weighted average of the trend growth rates of productivity γ and the real wage φ:
![]() (12)
(12)
which implies λ = γ = φ irrespective of the value of σ. However, when γ > φ and σ < 1 (12) implies λ > γ > φ.
Given that the typical estimate of σ is less than one and productivity has grown at a faster rate than the real wage, model based estimates of λ will exceed the observed trend growth rate of labour productivity and the real wage which is at odds with the underlying theory. In light of this finding we argue that Xt does not have a structural interpretation (that is, labour-augmenting technical change) and is best described as a reduced-form trend.
Another potential limitation of the basic deterministic trend assumption is that the trend growth rates of labour productivity and the real wage have varied significantly over time. As outlined in the Intergenerational Report 2007 (IGR), average labour productivity growth in Australia has varied significantly over the last four decades. Relatively strong growth was experienced during the 1970s and 1990s, while weaker growth was experienced during the 1980s and 2000s. Reflecting the conclusions of the IGR we allow for trend breaks in the estimation of Xt at 1980, 1990 and 2000:
![]() (13)
(13)
where:
T1980 = t for t (1980:1), = 0 elsewhere
T1990 = t for t (1990:1), = 0 elsewhere
T2000 = t for t (2000:1), = 0 elsewhere
D1980 = 1 for t (1980:1 to 2011:4), = 0 elsewhere
D1990 = 1 for t (1990:1 to 2011:4), = 0 elsewhere
D2000 = 1 for t (2000:1 to 2011:4), = 0 elsewhere
Estimation Results
Model with no trend
breaks
We begin by estimating the long-run relationship between employment, output and wages given by equation 8, treating Xt as a deterministic trend (see equation 10).
Table 1 reports that the slope of the reduced-form trend (λ) is 0.0165, implying 1.65 per cent average annual increase over the estimation period, with the elasticity of substitution between wages and capital (σ) of 0.33 suggesting that capital and labour are gross complements in the long-run. Augmented Dickey Fuller (ADF) tests applied to the model's residuals fail to reject the null hypothesis that the residuals of the long-run equation have a unit root (that is, it is not a cointegrating relationship) at a 5 per cent significance level.
Table 1: Two-step estimation: long-run results with no trend break
Method: Least Squares
Sample: 1972Q3 2011Q4
| Coefficient | Std. Error | t-Statistic | Prob. | |
|---|---|---|---|---|
| σ | -0.331177 | 0.035622 | -9.296944 | 0.0000 |
| μ | -0.554413 | 0.521788 | -1.062524 | 0.2897 |
| λ | 0.016569 | 0.000433 | 38.28854 | 0.0000 |
| R-squared | 0.993255 | Mean dependent var | 8.963825 | |
| Adjusted R-squared | 0.993168 | S.D. dependent var | 0.209544 | |
| S.E. of regression | 0.017321 | Akaike info criterion | -5.255027 | |
| Sum squared resid | 0.046501 | Schwarz criterion | -5.196876 | |
| Log likelihood | 418.1471 | Hannan-Quinn criterion. | -5.231411 | |
| Durbin-Watson stat | 0.276670 | |||
The second step is to estimate the coefficients on the short-run adjustment terms of the error correction model. Table 2 reports that the coefficient on the short-run adjustment term (δ) is -0.10, implying that 10 per cent of the gap between the actual and the desired level of employment closes per quarter. The coefficient on the first difference of log contemporaneous output (β1) implies that a 1 per cent rise (fall) in output is associated with a 0.12 per cent rise (fall) in employment. The coefficient on the lagged first difference of log employment (β2) implies that a 1 per cent rise (fall) in the lagged employment is associated with a 0.40 per cent rise (fall) in contemporaneous employment. The coefficient on the contemporaneous first difference of log real wages (β3) implies that a 1 per cent rise (fall) in wages output is associated with a 0.14 per cent fall (rise) in employment.
Table 2: Two-step estimation: short-run results with no trend break
Method: Least Squares
Sample: 1972Q4 2011Q4
| Coefficient | Std. Error | t-Statistic | Prob. | |
|---|---|---|---|---|
| δ | -0.104862 | 0.018585 | -5.642156 | 0.0000 |
| β1 | 0.115360 | 0.031948 | 3.610849 | 0.0004 |
| β2 | 0.402459 | 0.060669 | 6.633645 | 0.0000 |
| β3 | -0.140102 | 0.021724 | -6.449200 | 0.0000 |
| R-squared | 0.553914 | Mean dependent var | 0.004477 | |
| Adjusted R-squared | 0.545167 | S.D. dependent var | 0.005307 | |
| S.E. of regression | 0.003579 | Akaike info criterion | -8.402150 | |
| Sum squared resid | 0.001960 | Schwarz criterion | -8.324284 | |
| Log likelihood | 663.5687 | Hannan-Quinn criterion. | -8.370525 | |
| Durbin-Watson stat | 2.055190 | |||
Table 3: One step error correction model with no trend break
Method: Least Squares
Sample: 1972Q4 2011Q4
| Coefficient | Std. Error | t-Statistic | Prob. | |
|---|---|---|---|---|
| δ | -0.107599 | 0.018684 | -5.758732 | 0.0000 |
| σ | -0.437707 | 0.072869 | -6.006798 | 0.0000 |
| μ | -2.404735 | 1.508597 | -1.594021 | 0.1130 |
| λ | 0.017669 | 0.001164 | 15.17733 | 0.0000 |
| β1 | 0.117142 | 0.032008 | 3.659805 | 0.0003 |
| β2 | 0.375325 | 0.063015 | 5.956081 | 0.0000 |
| β3 | -0.144460 | 0.022191 | -6.509934 | 0.0000 |
| R-squared | 0.561641 | Mean dependent var | 0.004477 | |
| Adjusted R-squared | 0.544107 | S.D. dependent var | 0.005307 | |
| S.E. of regression | 0.003583 | Akaike info criterion | -8.381407 | |
| Sum squared resid | 0.001926 | Schwarz criterion | -8.245141 | |
| Log likelihood | 664.9405 | Hannan-Quinn criterion | -8.326065 | |
| Durbin-Watson stat | 2.026453 | |||
We now estimate the error correction model using a single step method. The estimated coefficients reported in Table 3 are similar to those estimated using the two-step approach. The elasticity of substitution between wages and capital is somewhat higher (in absolute terms) at -0.44, while the reduced-form trend's growth rate is larger at 1.76 per cent. ADF tests applied to the residuals of the long-run demand equation also fail to reject the null hypothesis that it is not a cointegrating relationship at a 5% significance level.
Model with trend breaks
Estimating the model with Xt as a linear deterministic trend generates long-run residuals that are clearly non-stationary with persistent deviations from zero occurring during the 1990s, when the Australian economy experienced a period of rapid productivity growth, and the subsequent slowdown in productivity growth during the 2000s. As discussed above, this may be due to breaks in trend labour productivity identified in the IGR, which we explore here by introducing decade long structural breaks in the reduced-form trend at 1980, 1990 and 2000.
Table 4: One step error correction model with three trend breaks
Method: Least Squares
Sample: 1972Q4 2011Q4
| Coefficient | Std. Error | t-Statistic | Prob. | |
|---|---|---|---|---|
| δ | -0.156972 | 0.023741 | -6.611907 | 0.0000 |
| σ | -0.333888 | 0.100664 | -3.316857 | 0.0011 |
| μ | -0.621929 | 1.460830 | -0.425737 | 0.6709 |
| λ2 | -0.002046 | 0.004556 | -0.449175 | 0.6540 |
| λ3 | 0.003265 | 0.003839 | 0.850405 | 0.3965 |
| λ4 | -0.008205 | 0.002600 | -3.155417 | 0.0019 |
| λ1 | 0.018097 | 0.002131 | 8.493971 | 0.0000 |
| β1 | 0.133119 | 0.031387 | 4.241247 | 0.0000 |
| β2 | 0.317678 | 0.064009 | 4.962995 | 0.0000 |
| β3 | -0.130795 | 0.023090 | -5.664621 | 0.0000 |
| R-squared | 0.595960 | Mean dependent var | 0.004477 | |
| Adjusted R-squared | 0.571223 | S.D. dependent var | 0.005307 | |
| S.E. of regression | 0.003475 | Akaike info criterion | -8.424715 | |
| Sum squared resid | 0.001775 | Schwarz criterion | -8.230050 | |
| Log likelihood | 671.3401 | Hannan-Quinn criterion | -8.345655 | |
| Durbin-Watson stat | 1.999231 | |||
Table 4 suggests that the trend breaks between the 1970s and 1990s are not statistically significant. Re-estimating the model with a single trend break at 2000 gives the following final set of estimates reported in Table 5.
The inclusion of the trend break results in a higher 'speed of adjustment' coefficient (δ) of -0.15. This implies that around 15 per cent of the gap between the actual and the optimal level of employment is eliminated each quarter. By comparison, Downes and Bernie's (1999) TRYM model estimate displayed a higher speed of adjustment of 19.8 per cent per quarter.
Table 5: One step error correction model estimation with one trend break
Method: Least Squares
Sample: 1972Q4 2011Q4
| Coefficient | Std. Error | t-Statistic | Prob. | |
|---|---|---|---|---|
| δ | -0.148297 | 0.021600 | -6.865504 | 0.0000 |
| σ | -0.400971 | 0.051069 | -7.851574 | 0.0000 |
| μ | -1.718589 | 0.933547 | -1.840923 | 0.0676 |
| λ2 | -0.005966 | 0.001500 | -3.977937 | 0.0001 |
| λ1 | 0.018457 | 0.000861 | 21.44554 | 0.0000 |
| β1 | 0.131177 | 0.031188 | 4.206066 | 0.0000 |
| β2 | 0.316862 | 0.063212 | 5.012681 | 0.0000 |
| β3 | -0.138063 | 0.021516 | -6.416706 | 0.0000 |
| R-squared | 0.593711 | Mean dependent var | 0.004477 | |
| Adjusted R-squared | 0.574623 | S.D. dependent var | 0.005307 | |
| S.E. of regression | 0.003461 | Akaike info criterion | -8.444641 | |
| Sum squared resid | 0.001785 | Schwarz criterion | -8.288909 | |
| Log likelihood | 670.9043 | Hannan-Quinn criterion | -8.381393 | |
| Durbin-Watson stat | 1.994711 | |||
Our estimate of the elasticity of substitution between capital and labour is 0.40, which lies at the lower of end of previous Australian estimates (for example, Debelle and Vickery (1998), Dungey and Pitchford (1998)). Again, Downes and Bernie's (1999) TRYM model estimate is somewhat larger at 0.82. The difference likely reflects the fact that TRYM incorporates greater capital/labour substitutability by modelling total hours worked and unfilled vacancies.
The estimated coefficient on the lagged first difference of log employment (β2) implies modest serial correlation, with a 1 per cent rise (fall) in employment causing a 0.32 per cent rise (fall) in employment growth next period. The estimated coefficient for contemporaneous output growth (β1) implies that a 1 per cent rise (fall) in output is associated with a 0.13 per cent rise (fall) in employment growth, and the estimated coefficient for real wages (β3) implies that a 1 per cent fall (rise) in wages is associated with a 0.14 per cent rise (fall) in employment.
ADF tests reject the null hypothesis that the residuals of the error correction term have a unit root at a 5 per cent significance level, which implies the long-run demand equation is a cointegrating relationship.
Finally, we explore the endogeneity of variables used in this analysis by estimating a vector error correction model using the cointegrating relationship estimated above. In light of Pagan and Pesaran (2008), we find that the three variable system (excluding the reduced form trend) can be usefully characterised by two trends (that is, the unit root processes governing output and the real wage) and one cointegrating relationship (that is, the long-run demand relationship with trend breaks). This analysis reconfirms the earlier finding of Dixon, Freebairn and Lim (2005) that output and the real wage are weakly exogenous to this system of equations thereby alleviating concerns relating to endogeneity bias.
7 This analysis updates the work of Gruen, Pagan and Thompson (1999) to 2011 data and finds that their estimates are preserved in the large data sample, with the 1980s characterised by large gaps between the actual unemployment rate and the NAIRU.