2. Theory

Date



Lewis and MacDonald (2002) and a host of others have demonstrated that long-run aggregate demand for labour in Australia is well-approximated by the first order condition for labour derived by solving a standard profit maximisation problem of a representative firm subject to a constant elasticity of substitution (CES) production function. The representative firm's profit maximisation problem can be presented as follows:

Equation 1: This equation describes the representative firm’s profit maximisation problem. Profits are defined as revenue (that is, output price multiplied by output) less labour costs (that is, wages multiplied by 1 plus the payroll tax rate multiplied by the number of workers) less the rental cost of capital (that is, the rental rate of capital multiplied by the stock of capital). Firms maximise profits by adjusting capital and labour inputs taking output prices, wages, payroll taxes, rental rate of capital, and output as given. (1)

subject to a constant returns to scale and CES production function:

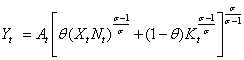Equation 2: This equation describes the representative firm’s production function. Production is assumed to take place according to a constant elasticity of substitution (CES) production function exhibiting constant returns to scale. Production requires the input of both labour and capital, with labour’s input multiplied by labour augmenting technical change. For completeness a scaling term is included to ensure the CES production function yields the historic level of output. This scaling term is effectively Hicks-neutral technological change. (2)

where: ∏t is profit at time t; pt is output prices; Yt is output (volume); wt is nominal wages; Mathematical figure is the payroll tax rate; Nt is employment; qt is the rental rate of capital; Kt is capital; At is Hicks-neutral technical change; 0 < θ < 1 is a weighting parameter; Xt is labour-augmenting technical change (Harrod-neutral); and σ > 0 is the elasticity of substitution between capital and labour.

For ease of exposition and without loss of generality, we assume that the firm's production function is always binding, which allows us to solve the following problem:

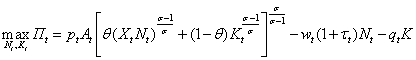Equation 3: Output is concentrated out of equation 1 by replacing output with the production function defined by equation 2. This substitution allows profits to be described by output prices, wages, payroll tax rate, rental rate of capital and the primary inputs (that is, labour and capital) which the firm can adjust to maximise profits. (3)

The resulting necessary first order condition for labour 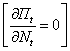Mathematical equation implies:

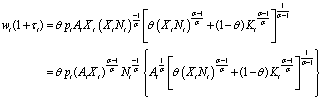Equation 4: This equation reports the first order necessary condition for profit maximisation resulting from equation 3, which is the point at which the derivative of profit with respect to labour input is equal to zero. (4)

Substituting (2) into (4):

Equation 5: This equation simplifies the first order condition in equation 4 by replacing the term that is equal to the production function with the level of output. (5)

and solving for labour (Nt) implies:

Equation 6: This equation makes labour the subject of equation 5. (6)

Taking logarithms gives the following labour demand relationship, conditional on the level of output, labour-augmenting technical change and real wages:

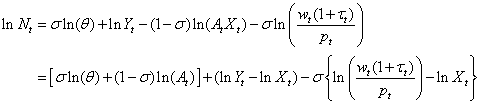Equation 7: This equation takes natural logarithms (hereafter denoted by log) of both sides of equation 6. The resulting equation yields a linear relationship of the following form: the log of labour is equal to a constant plus the log of Hicks-neutral technological change, plus the log of output minus the log of labour augmenting technical change, less the elasticity of substitution between capital and labour (denoted by sigma) multiplied by the log of the producer real wage (that is, the wage plus per-worker payroll tax divided by output prices) less the log of labour augmenting technical change. (7)

This expression can be simplified further by noting that there are no cyclical fluctuations over the long-run, so in the long-run At will be at its average level A, which yields the following long-run labour demand equation:

Equation 8: This equation is a simplified version of equation 7. Recognising that Hicks-neutral technological change is constant in the long-run, equation 7 can be re-written so that the log of labour is equal to a constant, plus the log of output minus the log of labour augmenting technical change, less the elasticity of substitution between capital and labour multiplied by the log of the producer real wage less the log of labour augmenting technical change. This equation is the paper’s definition on the long-run demand for labour. (8)

where: Mathematical equation

Equation (8) gives the logarithm of long-run labour demand as equal to three terms: a constant, the logarithm of real output adjusted for labour-augmenting technical change, and the elasticity of substitution multiplied by the logarithm of the real wage adjusted for labour-augmenting technical change (that is, the logarithm of long-run real unit labour costs). The effect of an increase in the level of labour-augmenting technical change on labour demand depends on the size of the elasticity of substitution between capital and labour: other things equal, labour demand decreases if σ < 1 and increases if σ > 1.