2.1 The discrete choice model of labour supply and child care
We estimate a discrete, structural model of the joint decision regarding hours of labour supplied by partnered women and household-level child care demand for families with pre-school children. The model assumes that households maximise their utility. Households get utility from consumption, leisure, and child development. Households choose hours of work by the mother, taking into account the trade-off between additional consumption which is made possible by working more hours but reduced leisure and time with children. Hours of formal child care are chosen to maximise child development and to free up the mother's time for work, but must be paid for at the market rate. We first discuss two important innovations in our paper: restricting the set of possible hours of work and child care to more realistically reflect labour market and child care conditions; and the relationship between hours worked, hours of formal care, and hours of paternal and informal care. We then discuss the technical implementation of our model.
2.1.1 More realistic labour and child care markets
The theoretical framework in this paper assumes that the decision about whether or not to work and how many hours to work for partnered women is made simultaneously with the decision of whether or not to use child care and how much child care to use. Blau and Robins (1988); Blau and Hagy (1998); and Connelly (1992) pioneered this approach, but these early papers assumed that hours worked and hours of child care demanded adjusted exactly to families' desires. For example, a partnered woman could choose to work 36 hours and if a small change in circumstances made it preferable for her to work 36.5 hours, she could adjust her labour supply exactly.
Our model is based on the standard discrete neo-classic labour supply model first developed by Van Soest (1995), but extended to include maternal child care as an explicit argument of the household utility function and to define the budget constraint over a small, discrete set of possible working hours and formal child care hours rather than over working hours alone. For example, an individual may choose to work 35 or 40 hours, but not a value in between these two points. (In practice, as described below, we allow eight different possibilities for working hours and six different possibilities for formal child care hours.) Families pick the combination of mother's working hours and formal child care that maximises their well-being from this set of 48 possible combinations of hours worked and hours of child care demanded. Kornstad and Thoresen (2007) estimate a similar model in that households are constrained in their choice of work and child care hours to a discrete set of points. However, our paper differs in the treatment of the relationship between formal child care and hours worked by the mother, as described below.
2.1.2 Formal child care, informal child care, paternal care and mother's working hours
In our model, we assume the following:
- During waking hours, children are cared for in one of four possible ways: by the mother; by the father; in a paid, formal child care setting; or in an informal child care setting. This last category will include care by other relatives or friends and may be paid or unpaid.
- In our model, we combine the father's time caring for children with informal care. This is partially driven by data restrictions. We do not observe hours or price of informal care. Nor do we observe hours of care by the father. In our model of the time allocation for mothers and children, therefore, these two types of care appear interchangeable. The model does allow for fathers to spend time taking care of children and allows the amount of time which fathers spend taking care of children to vary across households, but this care is not explicitly modelled.
- We assume that fathers' hours worked do not respond to changes in the price of formal child care or to mothers' wages. This is assumed for tractability of the model but also corresponds to evidence that mothers still bear a disproportionate share of time in taking care of children (Sayer, 2005; Kalenkoski et al., 2005). Kalenkoski et al. (2005) also confirmed a common finding that while women's market work responds to the presence of children, men's market work does not. Kimmel and Connelly (2007) modelled women's time spent in a variety of activities including home production and childcare and similarly treated fathers' behaviour as fixed.
- The household may choose to use formal child care regardless of whether the mother is at work or not. Formal care may exceed mother's working hours and may be used for purposes such as child development or freeing up time for the mother for activities other than paid work.
- We impose the restriction that total child care hours are at least as great as the hours of paid work by the mother and model informal and paternal child care as the difference between mother's working hours and formal child care hours. If formal child care hours equal or exceed mother's working hours, we assume that informal and paternal child care are zero. Otherwise, we set combined paternal and informal child care equal to mother's hours worked less hours in formal child care.3 Families will face different costs and benefits of informal care depending upon the proximity of grandparents or other relatives or the presence of other potential care-takers at home and we account for this in the model. Our approach is an improvement over Duncan et al. (2001) and Kornstad and Thoresen (2007) who assume, unrealistically, that formal child care hours must be greater than or equal to mother's hours of work. In our data, see below, about one-third of households report formal child care exceeding mother's working hours.
Figure 1 presents the household's decision over the allocation of the child's time. Sleep (the darkest shaded area) is treated as fixed and the family decides over the allocation of the remaining parts--how to split the remaining time into care by the mother, formal child care and informal/paternal child care.
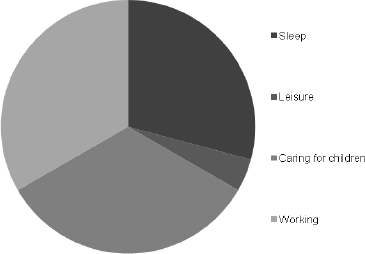
Figure 2 presents the mother's time allocation. After sleeping time, which is treated as fixed, mother's remaining time (the three most lightly shaded sections of Figure 2) is allocated between working, taking care of children, and leisure. Two `adding-up' constraints implied from (1) — (4) above must hold:
- Mother's time taking care of child = child's time being taken care of by mother
- Child's time in informal/paternal care = mother's working hours — child's time in formal care (or zero if this is negative)
Figure 1: Child's time
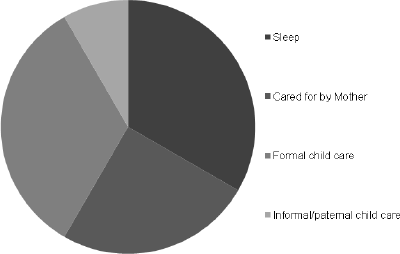
Figure 2: Mother's time
We further assume that, for mother
s with both pre-school and school–aged children, the primary consideration of the mother when she makes her labour supply and child care usage decisions is the well-being of the pre-school child(ren). That is, we assume that when school-aged children are present together with pre-school children in the same household, child care of the school-aged children outside school hours is assumed to mirror that of the pre-school children. Again, this is for tractability. For example, if formal hours of child care for the pre-school child are 40 and the school-age child is in school 30 hours per week then we assume that the school-age child is in before- and/or after-school care for 10 (40 less 30) hours per week. We test this assumption in two ways. First, we replace this assumption with an assumption that formal child care of school-aged children is fixed and does not enter the utility function. Secondly, we estimate the model using households with pre-school children only. We present these results in the Appendix and discuss them in section 4.2.3. None of the conclusions of the paper are sensitive to this assumption.
2.1.3 Technical specification of the model
The household is assumed to maximise a trans-log utility function by choosing consumption y mother's working hours h and formal child care hours cfi of each of her K children (indexed by i) from a set of discrete options:
(1)
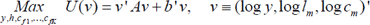
(2)
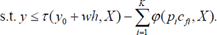
y is general consumption net of child care costs which is determined through the budget constraint (2) by asset income and father's income (both captured in yo), the mother's wage (w) and working hours, and the tax and transfer system which is captured by the function τ and which depends upon household characteristics, X.4 The function ϕ captures child care subsidies which depend upon child care costs (price, which may vary by the age of the child, pi multiplied by usage) and household characteristics. In addition to requiring that formal care of school-aged children be determined by the care needs of the pre-school children as described in 2.1.2 above, we also assume that all pre-school children use the same amount of formal care and pay the same price. This can be alternatively viewed as allowing differences in hours and price of care for pre-school children, but modelling the family's average demand.
lm is the leisure of the mother which is specified as the difference between her time endowment (Tm) and time spent either working or caring for children as in Figure 2 above
(3)
lm=Tc - h - cm'
cmis the time spent on maternal care which is specified as
(4)
cm= min{Tc - h,Tc - cf}
where Tc is the time during which children need to be cared for either by the mother, by the father, through the formal market or informally. Tc represents the three most lightly shaded sections of Figure 1.
The parameters of the utility function are summarised in A, a symmetric 3x3 parameter matrix with entries A, (i,j - 1,2,3), and b = (b1,b2,b3)', a vector with three parameters. b1 is a constant, but b2 and b3 are specified to allow both observed and unobserved individual and household characteristics to affect utility:
(5)
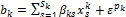 , (k=2,3)
, (k=2,3)
where xsk are exogenous characteristics including the age of the mother and the children, number of children in each age group, and other characteristics that describe the family composition such as the presence of extra female adults. In the case of multiple children, maternal child care is measured as the average number of maternal care hours for all pre-school children in the household and the impact of the number of children on utility is through b3. That is, the number of children affects the marginal utility of maternal care by shifting b3. (This explains why b2 ≠ b3 in equation (5) above. The k subscript on S allows for different characteristics to enter the two equations.) Moreover, the potential impact of informal child care is also allowed for by the inclusion of a dummy in b3 equal to one if h > cf. This dummy controls for which condition in equation (4) determines maternal child care hours and equals one if the family makes recourse to informal child care (as calculated by our residual measure of informal child care usage). The error terms εPk may be interpreted as random preferences due to unobserved characteristics.
Working hours and formal child care hours may take the following values:
(6)
h∈{0,8,16,24,32,40,48,56},
and
(7)
cfi∈{0,10,20,30,40,50}
These can be chosen in any of the possible 48 combinations, allowing a wide range of part-time and half-day possibilities for both work and formal care.
To estimate the model, we add random disturbances μj (as in Van Soest, 1995) to each alternative in the choice set, as in the multinomial logit model (Maddala, 1983):
(8)
Uj - Uj(yj,lmj,cmj) + μj (j = 0,…,48)
where μj's are independently and identically distributed with a type I extreme value distribution, and are independent of all observable and unoberservable terms in the model.
The mother chooses alternative j if it is the alternative (out of m*g=48) from which she derives the most utility, i.e. if μj is the largest among all the alternatives. Conditional upon εPk, X, and w, the probability that j is chosen is
(9)
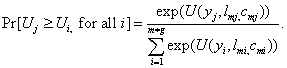
To predict the wage rates of non-workers and workers whose wages are missing in the data and to allow for correlation between wage rates and unobserved utility preferences (εPk), a wage equation is simultaneously estimated with (1) and specified as a standard Mincer wage equation:
(10)
log w = π'z=εw
where z is a vector of individual characteristics of the mother. Her education level, current area of residence measured by capital city and state, and a variable equal to one if the mother lived with both of her parents when she was 14 (to capture stability while growing up) are included in the wage e
quation but not in the utility function and serve the role of exclusion restrictions. π is a vector of parameters to be estimated. εw is an unobserved term, assumed to be normally distributed with mean zero, independent of z , but is allowed to be correlated with εPk.
As in similar models (for example, Gong and Van Soest, 2002), unobserved fixed benefit of not working (FB) is added to the income at zero hours of work. Thus the utility of all alternatives at zero hours of work are replaced by U(y0+FB,lm0,cm). FB is specified as
(11)
FB = δ't
where t is a vector of exogenous variables (which are listed in Table 2) and δ is a vector of parameters. Positive fixed benefits increase the probability of not working by increasing the utility of non-participation. They can be interpreted equally as fixed costs associated with working.
2.2 Estimation
If all the wages were observed and there were no unobserved preferences, the model could be estimated by maximum likelihood with the likelihood contribution given by Equation (9). With unobserved wages, the wage Equation (10) also needs to be estimated. This is done simultaneously with the joint labour supply-child care model. With the presence of unobserved preferences in leisure and maternal child care, maximum likelihood estimation would require evaluation of the three-dimensional integral defined over the distribution of the error terms εw, εp2, and εp3. Numerical integration in more than two dimensions can be difficult to solve.
We use Simulated Maximum Likelihood (SML) to avoid this multi-dimensional numerical integration. Denoting the probability of working hj hours and using cj hours of formal child care conditional on εp2, εp3, and wage rate5 by
(12)
Pr[h=hj,cf=cj|w,εp2, εp3] (j=l,…,48),
The exact likelihood contribution for someone observed to work h0 and use c0 hours of formal child care with observed gross wage rate w0 is then given by
(13)
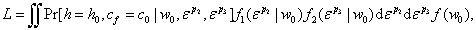
Or, if the wage rate is not observed, the exact likelihood contribution is
(14)
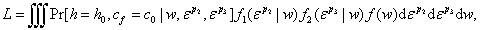
where  are the conditional density functions of εpkgiven w, and f(w) is the density of the wage rate (or of εw). The three error terms εw, εp2, and εp3are specified to follow a joint normal distribution of which the parameters are to be estimated:
are the conditional density functions of εpkgiven w, and f(w) is the density of the wage rate (or of εw). The three error terms εw, εp2, and εp3are specified to follow a joint normal distribution of which the parameters are to be estimated:
(15)
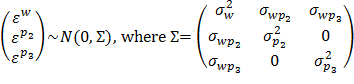
The numerical multi-dimensional integral is approximated by a simulated mean: for each individual, we take R draws from the distribution of the error terms (εw, εp2, and εp3) and compute the average of the R likelihood values conditional on these draws. The integral Equation (13) is thus approximated by
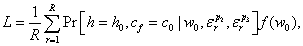
And Equation (14) is replaced by

where wr=π'z+εwr and (εwr, εp2r, εp3r) (r=1,…,R) are based upon draws from the distribution of (εw, εp2, εp3).
The draws are taken from Halton sequences using the procedure described in Train (2003). The estimator resulting from random independent draws is inconsistent for fixed R, but will be consistent as R tends to infinity with the number of observations of the sample.6 Many studies (see for example, Morokoff and Caflisch, 1995, Sloan and Wozniakowski, 1998, Bhat, 2001, Train, 2003, Sandor and Train, 2004) show that using 'quasi-random' draws which are designed to provide better coverage than independent draws, simulation can be more efficient in terms of reduced simulation errors for a given number of draws. In particular, Bhat (2001), Train (2003), and Sandor and Train (2004) all tested Halton sequences for mixed logit models and found their use to be superior to random, independent draws.
2.3 Simulations and the calculation of the net price elasticity
Labour supply and child care demand behaviour of households may be described by their corresponding elasticities. Due to the complexity of the model, simulation is needed to derive elasticities and to estimate policy effects. When calculating the elasticities, hours of work and child care are calculated as `expected hours', that is computed as a probability weighted sum of hours over all possible values which hours can take. Wage, gross child care price, and income elasticities for each observation are derived by increasing all wage rates, gross child care price, or other incomes by 1 per cent and calculating the percentage change of average expected hours or average expected employment rate. The net child care price elasticity is calculated as the ratio between the gross price elasticity and the percentage change in the net child care price corresponding to a 1 per cent change in the gross child care price. From these, we calculate the average elasticities for the whole sample and for selected subsamples of interest. The standard errors of these average elasticities are obtained using Monte Carlo methods by repeating the simulation 100 times with parameter estimates of the model drawn from their estimated distributions.
3 An alternative approach would be to use reported hours of informal care and to simultaneously model demand for formal and informal care alongside mother's labour supply. One immediate problem is that there is no information on price for informal care (in our data, only 10 per cent report paying for informal child care) even though families may incur non-pecuniary costs.
4 In τ,we include Newstart Allowance (NSA), Parenting Payment Partnered (PPP), Family Tax Benefits A and B, together with personal income tax, Medicare levy, and Low Income Tax Offset (LITO). Tables 2 and 3 list the variables that are contained in X.
5 Throughout, we condition on earnings of the husband, other non-labour income, child care price, and
other exogenous explanatory variables. These are suppressed in our notation.
6 If 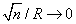 and with independent drawings across observations, the method is asymptotically equivalent to maximum likelihood (see Lee, 1992, or Gourieroux and Monfort, 1993 for references).
and with independent drawings across observations, the method is asymptotically equivalent to maximum likelihood (see Lee, 1992, or Gourieroux and Monfort, 1993 for references).