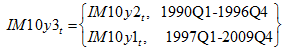4. Data and results



In our study the real interest margin is calculated in two ways. The first method is based on indexed bond yields:

 Indexed 10-year AUS government bond yield — Indexed 10-year US government bond yield

Since the data on US indexed Treasury bonds became available from 1997 Q1, this procedure can only obtain a sample from 1997 Q1 to 2009 Q4. The second method involves splicing separate measures of the real interest margin to obtain a longer sample (1990 Q1 to 2009 Q4).⁷ The real interest margin for the first part of this sample, 1990 Q1 to 1996 Q4, is calculated as:

 Indexed 10-year AUS government bond yield — (Nominal 10-year US government bond yield — 5-year US inflation expectations⁸)

The analysis will proceed with these two sets of measures for the real interest margin.⁹

The real interest margin for the longer sample can then be summarised as follows:

Data descriptions and sources are provided in Appendix 2.

Table 1 presents estimation results for both measures of the real interest margin, and . The estimations were conducted following a general-to-specific approach. Accordingly, the results only show statistically significant explanatory variables.¹⁰

While not included here, results from unit root tests indicate that most explanatory variables are unit root processes in level form and stationary in first-difference form.¹¹

Results for the real interest margin series from 1997 Q1 to 2009 Q4, , suggest no short-run link between government primary balances, either Australian or US, and the real interest margin, with only the US current account and Australian inflation appearing to exert a short-run influence on the margin. Surprisingly, the sign on the coefficient for Australian inflation is negative. This could potentially be explained by sluggish adjustment from inflation expectations to actual inflation outcomes.

Over the long-run, our results suggest that a one percentage point of GDP increase in the stock of Australian general government net debt is estimated to increase the long-run real interest margin by around three basis points — around one fifth that originally estimated by Comley et al. These results indicate that influences from the United States exert a far greater influence on the real interest margin than Australian influences. In particular, a one percentage point of GDP increase in the stock of US public net debt is estimated to decrease the long-run real interest margin by around nine basis points, while a one percentage point of GDP increase in the US current account balance increases the real interest margin by around 53 basis points.

Table 1: Results of the error correction model

	(1997Q1-2009Q4)	(1990Q1-2009Q4)
Explanatory variables: short run
Constant	2.839	5.178
	(5.347)	(6.414)
	-0.277	-0.205
	(-2.851)	(-2.151)
	0.197	0.322
	(3.249)	(4.545)
		-0.093
		(-2.682)
Error Correction Term	-0.415	-0.610
	(-7.024)	(-7.185)
Explanatory variables: long run
	0.025	0.028
	(2.180)	(2.830)
	-0.088	-0.098
	(-6.241)	(-11.479)
		-0.077
		(-2.347)
		-0.555
		(-7.362)
	0.533	0.471
	(6.790)	(7.884)
Adjusted R squared	0.588	0.531

Note: t-statistics in parentheses.

Results from the error correction model with the extended data series (1990 Q1 to 2009 Q4) are broadly similar. Government primary balances, both Australian and US, are found to be statistically insignificant in the short run. Overall, US factors appear to exert the largest influence on the real interest margin with a 1 per cent increase in the US current account balance estimated to cause the real interest margin to increase by more than 30 basis points in the short term.

The long-run results are again similar to those obtained from the smaller sample, and indicate that a one percentage point of GDP increase in the stock of Australian general government net debt increases the long-run real interest margin by around three basis points. A one percentage point of GDP increase in the stock of US public net debt is estimated to decrease the long-run real interest margin by around 10 basis points, while a one percentage point of GDP increase in the US current account balance increases the real interest margin by 47 basis points. Movements in the trimmed mean US inflation rate are found to exert a relatively large impact on the real interest margin, causing it to decrease by around 55 basis points in the long run for each 1 per c
ent increase in inflation.

One way of examining the robustness of these estimates is to investigate the unit root properties of the residuals from the implied long-run relationship of the error correction model. If there is a fundamental long-run relationship among the explanatory variables, the null hypothesis of a unit root should be rejected. By observing the stationarity of the residuals of the implied long-run relationship, we can also identify a plausible range for the estimates, potentially providing more useful information as opposed to the point estimates presented in Table 1.

This procedure is done by first estimating the error correction model to obtain the estimated coefficients. The model is then re-estimated after forcing the coefficient of the concerned variable to be a certain value above or below its estimated value. This is followed by an ADF unit root test for the estimated residuals of the implied long-run relationship. The ‘imposed’ coefficients for which the residuals remain stationary are taken as plausible fundamental estimates.

Essentially, we are interested in how sensitive the estimated residuals of the implied long-run relationship are to changes in the imposed coefficients of general government net debt, both for Australia and the US. To ensure that the actual estimates are covered, the range of the imposed coefficient on the government debt terms is chosen to vary from zero to 0.2, implying a range of zero to 20 basis points in the real interest margin resulting from a one percentage point of GDP increase in general government net debt. For illustrative purposes, these tests are only applied to the residuals of the implied long-run relationship in the case of the longer series of the real interest margin, . The results of these tests are summarised in Table 2.

Table 2: Unit root test on the residuals of the implied long-run relationship

Imposed coefficient of AUS_GGD,	ADF unit root test statistic
0.00	-6.396
0.05	-5.034
0.10	-2.936
0.15	-1.882
0.20	-1.303
Imposed coefficient of US_GGD,	ADF unit root test statistic
0.00	-2.233
-0.05	-3.835
-0.10	-6.081
-0.15	-3.889
-0.20	-2.193
Critical values
1% level	-5.28
5% level	-4.71
10% level	-4.43

Note: t-statistics are adjusted to correct for serial correction in the residuals (see Case 2 of Table B.9, Hamilton (1994)).

As indicated, the test for a unit root in the estimated residuals of the implied long-run relationship is rejected when the imposed coefficients are around their estimated values — implying the existence of a long-run relationship between the variables in the error correction model. The null hypothesis is also rejected at the 5 per cent significance level when the coefficient of the Australian general government net debt variable is five basis points or less. For the US, the estimated residuals appear to be only stationary when the coefficient of the US government net debt variable is around 10 basis points. These results suggest that it is reasonable to draw the conclusion that zero to five basis points is a plausible range for the change in the real interest margin for every one percentage point of GDP increase in the stock of Australian general government debt. For the coefficient of US government debt, around ten basis points seems to pass this residual-based robustness testing.

⁷ We note that the limited size of the sample implies some caution against putting undue emphasis on our point estimates.

⁸ The five year inflation expectations series is obtained from the University of Michigan’s Surveys of Consumers.

⁹ A third alternative would have been to calculate the real interest margin using nominal bond yields and inflation data. However, this alternative is less desirable given uncertainties about the relationship between inflation expectations and actual inflation. In addition, using this measure would make it difficult to distinguish between real and nominal impacts on the yield spread given that inflation is one of the explanatory variables.

¹⁰ The variables included in the table are statistically significant at a 5 per cent significance level.

¹¹ However, we note the relatively small sample size makes it difficult to test for unit roots with high precision.