The appropriate method to construct measures of uncertainty around forecasts depends on the way the forecasts were generated.5 As discussed in the Treasury Forecasting Review, there are a variety of approaches to modelling the economy. For example, one distinction between models is the trade-off between their coherence with economic theory and their coherence with economic data.
One approach could be to forecast using an economy-wide econometric model. In that case, it would be possible to use the model to generate measures of uncertainty around the forecast using statistics derived from that model. For example, suppose the forecasting model is:
AYt = BXt + et
where Y is the vector of macroeconomic and fiscal variables being forecast, X is the vector of other variables (such as historical data), A and B are matrices of parameters (which are estimated) and e is the vector of errors in the model.
Once this model is estimated over historical data, estimates of uncertainty can be generated around the forecasts based on the errors. For example, draws could be taken from the estimated errors and each draw used to calculate a forecast. This would generate a distribution of forecasts that would give a measure of uncertainty around the central forecast under the assumption that the future will experience similar shocks to those experienced in the past and that the structure of the economy will be similar in the future. Some of the issues and details around such an approach, known as bootstrapping, are discussed in Berkowitz and Kilian (1996).
In practice, however, many forecasters, including the Treasury, draw upon a combination of modelling techniques and a range of other information, including judgement, to produce forecasts. The use of a combination of approaches to produce forecasts reflects the judgement that each method has its advantages and disadvantages. For example, an econometric model is an imperfect representation of the world, so it may be desirable to adjust a model-based forecast with judgement (see the discussion in Office for Budget Responsibility, 2011).
In the absence of a single econometric model describing all key interlinkages between different aspects of the economy, it is not possible to use the above approach to provide reliable measures of uncertainty around the forecasts. This is because without a whole-of-economy model, which captures the relationships throughout the economy and the data-generating process of each variable, the impact of shocks on all forecast variables cannot be appropriately estimated.
However, to the extent that both the economy and the forecasting process used by a forecaster are similar to the past, uncertainty about a forecast can be assessed by the performance of similar forecasts in the past. Specifically, if the data-generating process for both the economy and forecasts is similar to the past, the forecast errors of the past will be a guide to future forecast errors. Reflecting this, a number of fiscal and monetary authorities have used their own historical forecast errors to derive measures of uncertainty (see Tables 1 and 2).
To construct confidence intervals (or prediction intervals) around the point estimate forecasts, we need to derive an estimate of the standard deviation of the forecast error.
For this, we calculate the root mean squared error (RMSE) for each forecast horizon:

where y f is the forecast variable, y is the actual outcome and the summation is over all n observations at that forecast horizon, s.6
Assuming the forecast errors are normally distributed with zero mean, the past is representative of the future and the variable y is stationary, confidence intervals can be calculated around the central forecasts:
Confidence Interval = y ft+s ± Z x RMSEs
where y ft+s is the central forecast and Z is the value of the relevant Z statistic for the confidence interval. For example, the 70 per cent confidence interval, used below, has a Z statistic of about 1.04, so the 70 per cent confidence interval is similar to the confidence interval of ± one standard deviation. Reporting the 70 and 90 per cent confidence intervals below gives a sense of the risks around the forecasts and follows the practice of the RBA.
When using the above approach for the forecasts of fiscal variables as a share of GDP (such as receipts as a share of GDP), the estimated confidence intervals will be affected by uncertainty in both the level of the fiscal variable (such as the level of receipts in dollar terms) and the level of nominal GDP. In the context of thinking about uncertainty around the level (or dollar value) of the fiscal variables, this can be misleading, as we will see shortly.
An alternative method of calculating confidence intervals, which reflects uncertainty only in the level of the variable, is to normalise the forecast errors by the actual outcome of GDP. To be specific, if we assume
![]()
where R is receipts, GDP is nominal GDP and ~N(0,σs2) means that errors are normally distributed with zero mean and constant variance, σs2 (so we are assuming the error in the forecast of receipts as a share of GDP is stationary) then the confidence interval is calculated as
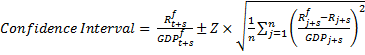 (1)
(1)
where the term under the square root sign is the maximum likelihood estimator of σs2. We refer to this as the no-GDP-error approach.
Taking account of the uncertainty about GDP in the confidence intervals around receipts (as a share of GDP) will tend to increase uncertainty (due to the variability of GDP), compared to the no-GDP-error approach which abstracts from GDP uncertainty, unless there is a positive relationship between errors in GDP forecasts and in receipt forecasts.
To explain this important point algebraically, the estimated variance of receipts as a share of GDP can be written as:
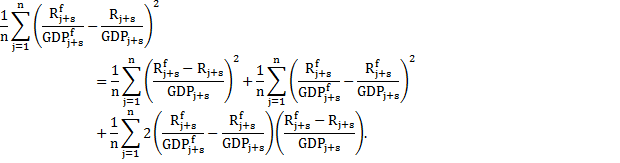 (2)
(2)
So the estimated variance of receipts as a share of GDP (the left hand side of the equation) can be decomposed into three terms. The first is the estimate of the variance using the no-GDP-error approach, the second is always non-negative and is a function of uncertainty around GDP and the third term reflects how GDP and receipt forecast errors are related. If over-predictions of GDP are usually associated with over-predictions of receipts (and similarly for under-predictions) then this third term will be negative.
We will see below that the confidence intervals around receipts as a share of GDP using the no-GDP-error approach are larger than those which take account of uncertainty in nominal GDP, reflecting the strongly positive relationship observed between forecast errors for nominal GDP and for receipts.
To understand this point, consider the (extreme) scenario in which there are large errors in the forecasts for the levels of both receipts and GDP, but these errors are perfectly correlated so there is no error in the forecasts for the receipts-to-GDP ratio. In this case, there would be no confidence interval around the forecast ratio of receipts to GDP, which would clearly not be representative of the confidence intervals around the level of receipts. To generalise the point, small variances in the forecast e
rrors of the receipts-to-GDP ratio can correspond to large forecast errors in the level of receipts when there are also large nominal GDP forecast errors. With the no-GDP-error approach (which does not allow for any error in the GDP forecast in the denominator of the receipts to GDP ratio), the error in the ratio is driven entirely by errors in forecasts for receipts, regardless of their causes (including GDP forecasting errors).
By contrast, the confidence intervals around payments as a share of GDP using the no-GDP-error approach are smaller than those which take account of uncertainty in nominal GDP, reflecting the negative relationship observed between forecast errors for nominal GDP and for payments.
The assumptions that the forecast errors are normally distributed with mean zero may not be exact, though it or similar assumptions are often made in generating confidence intervals (see Tables 1 and 2). Table A1 (in Appendix A) presents some summary statistics which shed light on the extent to which the assumptions are satisfied for the sample of historical forecast errors used in the calculations below (see below for information on how variables have been constructed and other details about the data).
Our analysis indicates that, in this sample, there are some signs of bias, with a tendency to under predict nominal GDP growth and over predict payments (Table A1). However this particular sample may be unrepresentative of the population or of future forecasts. Examining a longer sample suggests that Treasury's real GDP, nominal GDP and revenue forecasts exhibit little evidence of bias for the Budget year (Treasury, 2012). Moreover, even if there is systematic bias in our particular sample, forecasters are expected to learn and adjust their forecasts. So, any bias in errors is unlikely to persist.7 Table A1 suggests that it is difficult to reject the hypothesis that the errors are normally distributed in our sample. This is consistent with the forecast error being the average of many miscellaneous factors and so by a central limit theorem the forecast errors should be approximately normally distributed.
The assumption that the future is similar to the past is also important. While this is not testable, confidence intervals generated using this assumption provides a useful guide to likely risks around the forecasts.
5 An alternative approach would be to report subjective estimates of uncertainty. However, many studies have found these to be too low, often by large margins (see Tulip and Wallace, 2012).
6 In the analysis below for the Australian budget, the horizons are the financial year that is about to end and the two subsequent financial years. For the 2013-14 Budget delivered in May 2013, these correspond to 2012-13, 2013-14 and 2014-15.
7 Generally the amount of serial correlation in the errors is statistically insignificant, though there are some signs of serial correlation in our sample for the forecast errors for receipts as a share of GDP.